by DemiPixel

Exact Solution for “Exact Change”

NOTE: If you’re working through Free Code Camp and haven’t completed this problem, I really recommend try it first!

I was messing around with Free Code Camp and was challenged by someone to try and correctly complete the “Exact Change” problem.

The Problem

The Exact Change problem asks you to write a function that outputs the least amount of coins to add up to a given amount of money and a given 2D array of coins formatted something like:

[[“PENNY”, 1.01], [“NICKEL”, 2.05], [“DIME”, 3.10], [“QUARTER”, 4.25], [“ONE”, 90.00], [“FIVE”, 55.00], [“TEN”, 20.00], [“TWENTY”, 60.00], [“ONE HUNDRED”, 100.00]]

Notice how it shows we have $1.01 in pennies instead of stating “101 pennies”.

Incorrect Solution

So Free Code Camp is for beginners, so I can understand that the answer they provide would be most intuitive for people trying to understand how it works. Unfortunately, the algorithm does not always have the desired effect. You can see the full code snippet here, but this is a short summary of what it does:

coinList = []

for each denomination    while amountLeft < coinValue && coinLeft > 0        Add the coin to coinList        coinLeft--        amountLeft -= coinValue

if (coinList.length == 0 || amountLeft > 0)  return "Insufficient Funds"otherwise return the array

And while this may seem like a simple and brilliant solution, we run into some issues. I was challenged specifically for the following test:

$0.30 with dimes and quarters

Let’s say we want to get $0.30 with 10 dimes and 10 quarters (so we have more than enough dimes or quarters). This is where the previous algorithm trips a bit.

The method it uses is to use the highest denomination and go down until it reaches the goal or the lowest denomination. It first tries to use a quarter (since that is the highest available denomination) and is left with $0.05.

Since amountLeft (amount of money left to make with coins) is > 0, it returns “Insufficient Funds” because a dime is more than $0.05 and there are no other denominations left. However, we all know that the correct solution is to make $0.30 with three dimes!

We can’t start from the lowest denomination and work up (such as start at dimes, then go to quarters) because we might run into a problem like $0.40 with 1 nickel, 3 dimes, and 1 quarter.

The program will start by trying to use the nickel ($0.05, lowest denomination), then the 3 dimes ($0.35, second denotation to use), and will return “Insufficient funds” because we can’t make our remaining $0.05 with dimes nor quarters. It wasn’t trying 1 nickel, 1 dime, and 1 quarter (which makes $0.40 exactly).

Smaller Problems

Let’s start simple. How could we do the problem if we wanted the coins to make $0.01? Well, we go through the denominations and check to make sure we have enough of that coin (i.e. enough pennies) and than coin is worth <= $0.01 (which a penny is).

Now let’s look at $0.02. For humans, it’s easy to see that $0.02 is simply two pennies away from $0.00.

However, for a computer, it’s not that simple. What we can do for the computer is to express reaching $0.02 as “1 penny more than $0.01”. We can also express $0.03 as a penny more than $0.02.

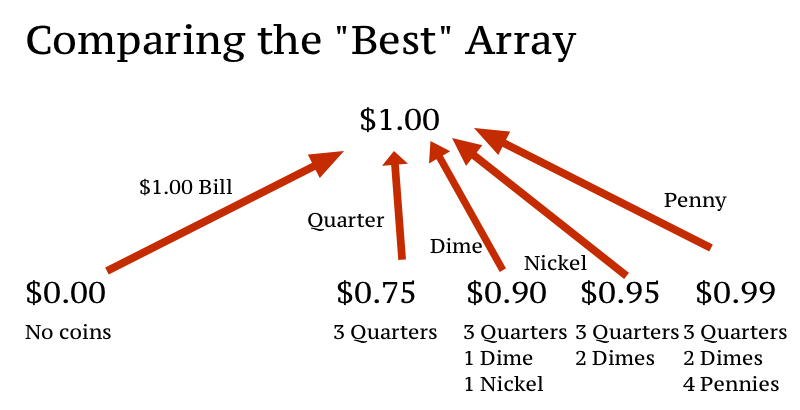
A larger example would be with $1.00. $1.00 is a penny + $0.99 or a nickel + $0.95 or a dime + $0.90 or a quarter + $0.75 or a dollar bill + $0.00. Since a five dollar bill is greater than $1.00, we simply ignore it (and any higher denotations).

So if we go back to our original problem and want to calculate $0.30 from dimes and quarters, we first need to calculate and save the combination of coins to make $0.01. Then calculate and save for $0.02. Then for $0.03, $0.04, $0.05, and so on until we get to $0.30.

Each time we want the next value (for example $0.20), we look at the the value of $0.20 and subtract the coin type we’re on in the denomination loop (e.g. a dime).

This leaves us with $0.20 minus a dime, which is $0.10, and we can simply say “add a dime + the coins that make up $0.10”. This will likely be represented as an array of coins, so imagine that $0.10 is [‘dime’]. Since we are saying that “a dime + the coins that make up $0.10” gives $0.20, we can say that $0.20 is [‘dime’, ‘dime’] because we’re adding an extra coin (the dime) to our list.

Perfect! $0.20 is two dimes.

Best Value

If we go back to our $1.00, we have lots of ways of achieving the same value. How do we know which is the best? How do we know if it’s better to use a dollar bill, or better to use a dime + $0.90 in coins? We could say “the largest denomination is the best”. Since the one dollar bill is our largest useable denomination, we would simply state that the one dollar bill is the best choice (and set $1.00 to [‘1 dollar’]).

So what about $0.30 given 5 pennies, 3 dimes, and 1 quarter? Using the “largest denomination” method, we would try and make $0.30 from either “dime + $0.20” or “quarter + $0.05”. It looks like quarter is the better option (quarter + $0.05), when in reality that gives us a six coin answer (quarter and five pennies), when we want a three coin answer (three dimes)!

What we really want is to compare the number of coins. Since there are less coins in $0.20 (two dimes) than there are in $0.05 (five pennies), the $0.20 + dime would be the optimal choice for $0.30.

In Practice

Since we’re just finding the best value for $0.01, then $0.02, then $0.03, so on and so forth, we can simply use a for-loop instead of recursion or a while loop!

Now, in reality it would be impossible to store the values as [‘dime’, ‘dime’, ‘quarter’] like I stated above. The way I stored it was with an array of integers, in the format [pennies, nickels, dimes, quarters, etc]. So 3 quarters and 2 dimes would be [0, 0, 2, 3, 0, 0, 0, 0] (goes up to $20 bill since that’s the maximum denomination in the problem).

In my code, I call the number of coins a “score”. If you’re not familiar with it, O(_), it’s a format that allows programmers to show how efficient a specific program is, and how well it will perform when scaled up.

Now, I wanted the algorithm to be O(money*denominations), however having to recalculate the score every time would make it O(money*denominations^2). What I decided to do was simply create another variable to store the score like I am storing the best amounts. So, if I wanted $0.30 from a dime + $0.20, I could look at bestScoreList[$0.20] and see that it gave the value “2”.

Since a dime is one coin, we just do bestScoreList[$0.20] + 1 which is 3. If this confuses you, don’t worry. Just remember that bestScoreList[i] (ex value: 5) is going to save the number of coins in best[i] (ex value: [2, 0, 3, 0, 0, 0, 0, 0]) without having to always recalculate it.

Lastly, in our $0.30 problem, we get to $0.20 + a dime or $0.05 + a quarter. Since $0.05 is 0 coins (since there’s no way to get $0.05 from quarters and dimes), it states that 1 quarter is the best solution.

The best way to counteract this is to simply ruin the score if the score is 0 and it’s not accessing $0.00. For example, $0.10 with a dime might return a score of “1” because $0.00 has a score of 0, and therefore it adds 1. If, however, we have $0.15 with only dimes, it would return a score of “0” because $0.05 has a score of 0 (no way to make $0.05 with dimes!) and $0.05 is not $0.00 (obviously).

We ruin the score because it means it’s an impossible solution (since we want to reach $0.00 and that’s not possible with this specific denomination).

Code

Here’s the code and a test case of the $0.30 with dimes and quarters problem. It uses a bit of ES6, so change that if you can’t use that for some reason. Also note that the problem gave “cash given” (in cash) and “price of item” in price. This means that we’re actually looking to give them cash-price coins. Here it is!